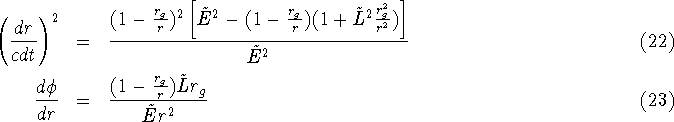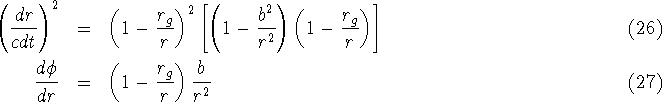Einsteins field equations and Black Holes

Historical Background

All metrics describing a physical system should satisfy Einstein's field equations:

Einstein himself, used them to calculate the precession of Mercury, by an approximation method. He got the result from the Newtonian theory in the first approximation. The second approximation explained - correctly - the deviations from that theory. But the calculations was not so clear, so the mathematician Karl Schwarzschild went for an exact solution. In his own words (in [7], p. 452):
"It is always pleasant to have at one's disposal
a rigorous solution of simple form"

At that time he was serving in the German army on the Russian front of World War I. After a few days of calculation he had found the exact solution of the problem proposed by Einstein. He mailed his paper "On the Gravitational Field of a Point Mass according to Einsteinian theory" to Einstein in 1916, and within a half year he died because of illness catched in the war (see [8] p. 124). The application of Einsteins field theory was now much more clear, but no one imagined what kind of object the metric fully described: a star which holds everythin back including light.

The idea of these black stars was already conceived 200 years ago - in 1795 by Pierre Laplace. He thought of a star 250 times larger than the sun, which would hold all light rays back and thereby being invisible. (see [6] p. 7).
In 1963 Roy Kerr found the solution to Einsteins field equations describing spinning stars. Within a year, Robert Boyer, Richard Lindquist, Roger Penrose and Brandon Carter proved, that Kerr's solution actually described spinning Black Holes, and in fact every spinning Black Hole that can possibly exist!

Schwarzschild's spherical symmetric Black Holes

The Schwarzschild metric describes the spacetime of a spherical symmetric point mass (an arbitrary star) in vacuum. With (or if G=c=1) it is written:

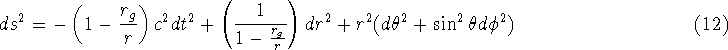
where M is the mass of the object (included in ) and G is Newton's gravitational constant. The metric depends only on r and is fully determined by M. For large distances ( ) the metric describes flat Minkowski spacetime: . If all the mass is concentrated inside the gravitational radius, we have a spherical symmetric Black Hole, where all the geometric distortion effects can be experienced by falling particles... In this section we will look at the curvature, the redshift-effects and celestial mechanics in the vicinity of the Black Hole. We will start with the curvature.

Curvature

The curvature of the Schwarzschild metric depends only on r, because of the sperical symmetry. The scalar curvature R is contracted from the Riemann curvature tensor, and the result is in units of the gravitational radius:

Sometimes it is written: (if you set G=c=1 so ). (See eg. Misner Thorne & Wheeler [3] p. 822). The full calculation of C requires tensor calculus en masse.

How does this curvature function look?

 
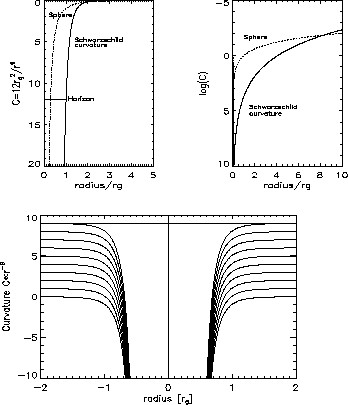
Figure 3: (a), (b) The curvature of the Schwarzschild spacetime compared with the curvature of a sphere. The curvature goes to infinity (shown downwards) very quickly. (c) Layers of space at successive points in time forms a spacetime-sandwich.

Most people know of the rubber sheet analogy where the sheet of rubber is curved because of a heavy bowlingball. First we will look at the curvature compared to the curvature of a sphere:

It is really going to infinity for . And all the mass is located in this singularity. You could say that all motion is due to the curvature of space which is caused by the point mass. Let's draw a number of curvature profiles on top each other representing successive points in time. The timearrow hits the next profile sooner and sooner, the larger the curvature. Time "stops" because all future space planes is coinciding with the present space. The "sandwich" of spacetime is made of thinner slices. On the other hand, the physical distance dx travelled when moving one time step from one plane to the next, becomes larger and larger. The lightcones are flattened and will look like pancakes!

If we take a slice of the 3D-space (for example the equator plane), we can show the curvature of the surface in an embedding diagram; see figure 2.3. We know, that time is always orthogonal to space, so we place a lightcone in each grid point of the polar coordinate system (it could be Cartesian as well). The green lightcones (pointing up) represents the future and the red lightcones (coming up) represents.

  
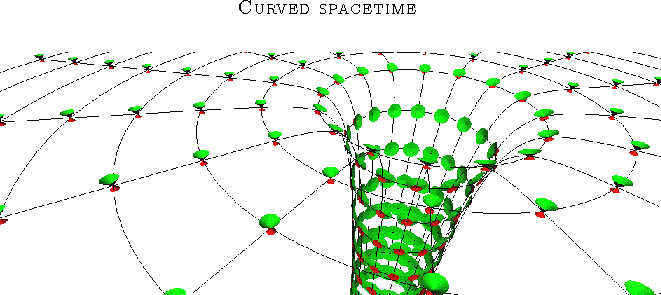
Figure 4: Embedding diagram showing one slice of the spherical symmetric spacetime of a Schwarzschild Black Hole. Space is curved like a sheet of rubber with a heavy bowling ball. The lightcones (green: future, red: past) are deformed when the curvature is increased - they get larger in the space coordinate and smaller in the time coordinate near the horizon. Note that the past-lightcones are shown with the half time step.

Radial motion and gravitational redshift

The Schwarzschild metric is often written with where as usual. The factor is called the redshift factor. We can understand this by some simple considerations.

First we will find the proper time : (see [1])

We notice, that becomes zero at the gravitational radius (time "stops"), and of course for a distant observer. In the same way we find the physical distance dx:

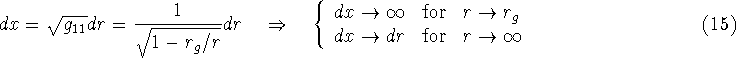
The physical distance of a relativistic particle (eg. a photon) travelling close to the gravitational radius becomes greater and greater (because of the curvature of spacetime). For distant observers - in spacetime far from - the distance is "untouched". To calculate the redshift, we can find the radial motion of a photon (which has always the velocity c). For all ultra-relativistic particles (including photons) the separation ds=0. In the case of radial motion, in the Schwarzschild metric:

which gives the equation of motion for the coordinate velocity:

where is the velocity in coordinates of a distant observer, while is the physical velocity of the photon in proper units. The distant observer would see light "slowing down" as , because the change dx, in physical distance, with his clock-ticks dt is:

The photon energy - or it's frequency - changes while approaching the center. We consider light that flashes with the time interval (eg. the red light on the back of a small space-craft). The light is emitted at a point and is observed at after the same interval . Now where and similarly. This gives the shift in frequency:

The frequency decreases ( ) if the quantum leaves the gravitational field ( ). Decreasing frequency means increasing wavelength equal to a redshift. On the other hand, when the quantum moves towards the center, it is blue-shifted. We could apply this formula to a small space-craft moving towards the center, where the unfortunate observer is looking out of the rear window to the safe universe where he came from. What will he see? The light from the distant stars (one of which was his home) with will be shifted like:

and will become more and more blue when . The situation will be opposite if we are located in a safe stable orbit around the Black Hole, observing the red lights of the falling space-craft. Now and , so:

This will only hold until the space-crafts reaches the horizon at where the red lights will be infinite redshifted far beyond infrared and thus invisible. In terms of the redshift factor it becomes very simple: where . We will take advantage of this simple form when considering redshift in the Kerr-metric, where the depends also on the rotation parameter a.

Celestial mechanics

We will now consider the motion of test particles along geodesics (the analogy of straight lines in flat space). This is investigated by letting particles fall freely in the spherical symmetric gravitational field described by the Schwarzschild metric. In this case, the symmetry reduces the problem to a movement in one dimension (the radial component). The equation of motion is (see [1] p. 28-32):

Where is the specific energy of a particle (in units of ); this is relatted to the physical velocity v:

is the specific angular momentum (in units of ).

  
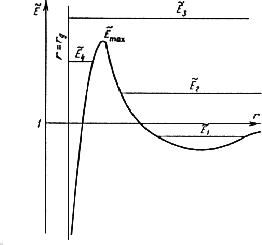
Figure 5: The effective potential for constant angular momentum . There are 4 types of motion.

From (22) we can find the point of maximum approach (minimum distance) of a test particle moving from it's maximum distance towards the center. Setting we find:

This equation defines the effective potential for the particles. There are 4 different types of motion, see figure 5 and table 3:

  
Table 3: The type of motion depends on the energy of the particle. The radius intervals refers to radii ( to ) not shown on the figure. These values are found where the horizontal lines hits the effective potential.

The orbits corresponding to these types of motion are shown in figure 6:

  
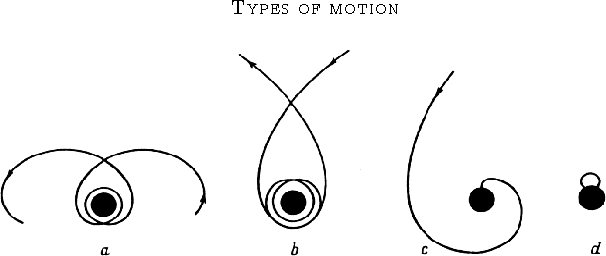
Figure: The types of motion corresponding to table (2.5) and figure (2.5). From left: (a) - bounded motion (precessing ellipse), (b) - hyperbolic motion, (c) - gravitational capture, (d) - gravitational capture from horizon.

In addition there are two types of circular orbit located at the two extrema in the diagram. For the orbit is unstable, and for the orbit is stable.

For other values of the effective potential changes. Typical values are and . does not have an extremum for , and therefore circular orbit is impossible below this value.

In the case of ultrarelativistic particleis (eg photons) we consider equations (22) and (23) in the limit: . We cannot use and because they tends to infinity. Instead we parametrise by and find (see [1] p. 32):

These equations of motion describes a light beam moving close to a Black Hole. We can find the extremum points on the trajectory b(r) analogue to .

  
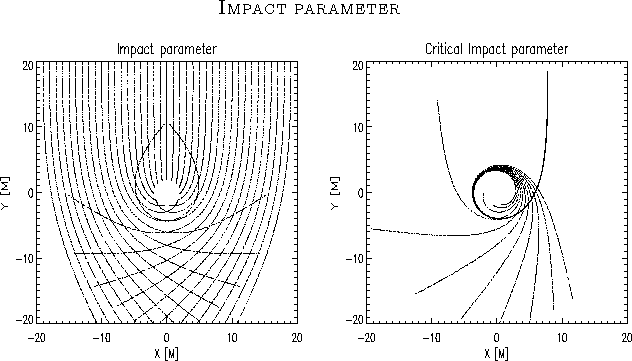
Figure 7: The geodesics are deflected for large impact parameters, and captured for small impact parameters. For a critical impact parameter, only small deviations separate trajectories which are captured from those which are rejected in an arbitrary direction. The axis shows X and Y distance ("radius") in units of M, where (G=c=1).

As in the case of relativistic particles, the ultrarelativistic particle can reach a minimum value in r before receding to infinity; it can also go a number of times round before it leaves the Black Hole. The impact parameter is a function of the tangent of the angle between the trajectory and the direction to the center of the Black Hole. The critical impact parameter ( ) defines when the particle is (gravitational) captured. If the particle will fall into the Black Hole.

The plots in figure 7 shows the deflection of ultrarelativistic particles send towards a Schwarzschild Black Hole with different impact parameters.