Mathematical Formulation of the Yilmaz Theory of Gravity
Due to Albert Einstein, we have learned that the effect of gravitation can be
interpreted geometrically as curvature of space-time.
Mathematically, this is expressed in the Einstein equations [6]
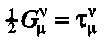
where the lefthand side denotes the Einstein-Hilbert curvature tensor and
the righthand side is the stress-energy tensor of the source fields
(matter, electromagnetical...).
The new theory of Hüseyin Yilmaz can still be interpreted
geometrically. What differs to general relativity is that the
stress-energy-momentum of the gravitational field itself is assumed to
be a source of curvature. Thus, the conventional theory of gravity has
to be modified by adding
the stress-energy tensor of the gravitational field to the righthand
side of the Einstein equations [1]:
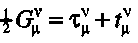
C. O. Alley states that he "believes that
the explicit inclusion of the gravitational
field stress-energy tensor [...] is as important for our understanding
of physics as Maxwell's addition of the displacement current in his
equations for the electromagnetical field" [2].
If one starts from the space-time metric, then the gravitational
potential 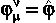 is defined (up to integration constants) according to
is defined (up to integration constants) according to
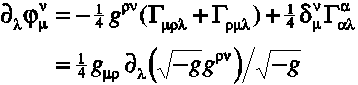
with 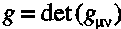
However, the geometrical interpretation of the new theory is not the
essential one. Remarkably, the new theory is a gauge theory very similar
to electromagnetism (see below). The Lagrangian of the free field (no
other sources) is given by
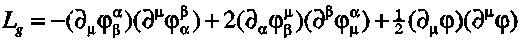
with  . The
energy-momentum tensor of the gravitational field then follows
by variation of the Lagrangian as
. The
energy-momentum tensor of the gravitational field then follows
by variation of the Lagrangian as
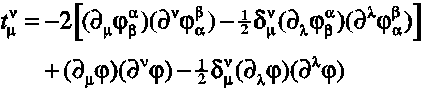
The inverted relation between the gravitational field and the space-time
metric is formally exponential
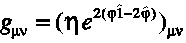
The greek symbol eta represents the matrix of the usual
metric of special relativity (Minkowski metric).
Differences to General Relativity
The new theory of gravity seems to resolve some flaws of general relativity
- There is local conservation of energy-momentum, as a definite
stress-energy tensor can be assigned to the gravitational field.
- In the solutions of the field equations there appear no space-time
singularities and there are no "event-horizons", in contrast to general relativity.
Thus, Yilmaz's theory of gravity does not predict the existance of black
holes. It is worth noting that Albert Einstein himself
could never believe in the reality of black holes - he considered them
to represent rather a mathematical anomaly than real objects.
Then, the new theory has some more advantages:
- The new theory is compatible with all experimental data (what it
is essential, of course).
- The strong equivalence principle, which means the equivalence of
inertial mass, active gravitational mass and passive gravitational mass,
is a direct consequence of a multiplicative gauge invariance.
The equivalence principle is not deducible in Einstein's theory, where it
has to be included as an additional assumption.
- There exist closed solutions for gravity waves for arbitrary field
strengths. The wave equation (see below) is exactly satiesfied, and not
only in the weak field limit as in general relativity.
-
Remarkably, H. Yilmaz also claims to have found a way to
quantize the theory. Usually, gauge theories with non-polynomial
Lagrangians (as is Yilmaz theory) are considered to be non-quantizable,
because they are known to be non-renormizable. Surprisingly,
H. Yilmaz found a way to avoid this obstacle. By applying some simple physical
principles, he claims to have discovered a quantization method
which renders the usual renormalization procedure superfluous [4,5].
| Theories of Gravity
| Albert Einsteins
General Relativity
| Hüseyin Yilmaz
Theory of Gravity
|
| Type of theory
| no gauge theory
| gauge theory
|
| Local conservation of enery-momentum?
| No
| Yes
|
| Definite stress-energy tensor exists?
| No
| Yes
|
Exact closed gravity wave solutions
for arbitrary field strengths?
| No
| Yes
|
| True Lagrangian exists?
| No
| Yes
|
Interaction can be deduced from gauge
principle?
| No
| Yes
|
| Strong principle of equivalence?
| Not deducible
| Holds
|
| Theory is quantizable?
| No(?)
| Yes(?)
|
Can be interpreted geometrically
(as curvature theory)?
| Yes
| Yes
|
Solutions with space-time
singularities ("black holes")?
| Yes
| No
|
| Compatible with all observations?
| Yes(?)
| Yes(?)
|
Correspondence to Maxwell's Theory of Electromagnetism
The similarity between the new theory of gravity and electromagnetism is
really striking. With suitable coordinate and/or gauge conditions the field
equations are analoguous, except that there appears an additional index for
the gravity theory. Moreover, the interaction with other
fields can also be deduced from a gauge principle, ie. by
replacing ordinary derivatives with gauge-covariant derivatives in the
Langrangian. While the gauge is additive in electromagnetism, the new theory
of gravity satisfies a generalized multiplicative gauge.
|
| Electromagnetism (Maxwell's theory)
| Yilmaz Theory of Gravity
|
Field equations
(Lorentz gauge)
| 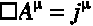
| 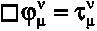
|
| Gauge transformations
| 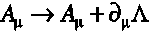
| 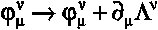
|
| Gauge-covariant derivatives
| 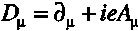
| 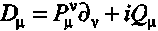
|
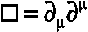 denotes the d'Alembert operator.
In the Lorentz gauge
the potentials of the new theory thus satisfy a standard wave equation.
denotes the d'Alembert operator.
In the Lorentz gauge
the potentials of the new theory thus satisfy a standard wave equation.
Outlook
Although the new theory does surely not represent the last word concerning
gravity, I think that it still can be viewed as a valid alternative to
general relativity, although, naturally, there have been many
controversial reactions [7].
References
[1] H. Yilmaz: "Towards a field theory of gravity", Nuovo Cimento 107B
(1992), pp. 941
[2] C. O. Alley: "Investigations with lasers, atomic clocks and computer
calculations of curved spacetime and of the differences between the
gravitation theories of Yilmaz and of Einstein", Frontiers of Fundamental
Physics, edited by M. Barone and F. Selleri,
(Plenum Press, New York, 1994),
p. 125-137
[3] H. Yilmaz: "Did the apple fall?", Ibid, p. 115-124
[4] H. Yilmaz: "Gravity and quantum field theory: A modern synthesis",
Fundamental Problems in Quantum Theory, Annals of the New York Academy
of Sciences 755 (1995), p. 476-499
[5] C. O. Alley: "The Yilmaz Theory of Gravity and Its Compability with
Quantum Theory", Ibid, p. 464-475
[6] S. Weinberg: "Gravitation and Cosmology", (Wiley, New York, 1972)
[7] J. Horgan: "Bashing Black Holes: Theorists twist relativity to
eradicate an astronomical anomaly", Scientific American,
July 1995, 11
[8] F. I. Cooperstock, D. N. Vollick: "The Yilmaz challenge to general relativity",
Nuovo Cimento 111B (1996), 265
[9] E. D. Fackerell: "Remarks on the Yilmaz and Alley papers", Proceedings of the first
australasian conference on general relativity and gravitation, ed.: D. L. Wiltshire,
University of Adelaide (1996), 117;
![]()
![]()
![]() is defined (up to integration constants) according to
is defined (up to integration constants) according to
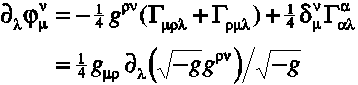
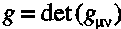
![]()
![]() . The
energy-momentum tensor of the gravitational field then follows
by variation of the Lagrangian as
. The
energy-momentum tensor of the gravitational field then follows
by variation of the Lagrangian as
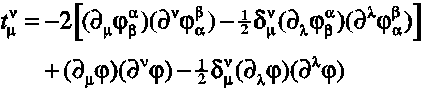
![]()
![]() denotes the d'Alembert operator.
In the Lorentz gauge
the potentials of the new theory thus satisfy a standard wave equation.
denotes the d'Alembert operator.
In the Lorentz gauge
the potentials of the new theory thus satisfy a standard wave equation.